La maldición de la multidimensionalidad
Posted on 15 Sep 2017
La maldición de la dimensionalidad es el efecto por el cual muchos problemas matemáticos se vuelven difíciles cuando tratamos con muchas dimensiones. En este artículo explicamos por qué en altas dimensiones una caja con un melón contiene más aire que melón, por qué la vida se complica con muchas dimensiones y cuáles son algunos efectos de la maldición en estadística y en aprendizaje automático.
Moscas multidimensionales
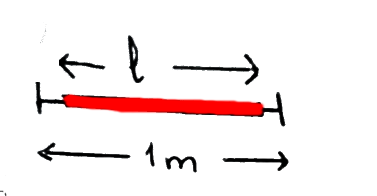
Minsky es un robot unidimensional que vive en un universo contenido en un segmento de 1 metro. Un día, el robot ve una mosca que vuela hacia delante y hacia atrás en el segmento. Minsky decide cazarla con su cazamoscas, que tiene una longitud de \(l = 0.8\), Como Minsky no tiene ni idea donde estará la mosca en un momento dado, lanza su cazamoscas a boleo. La probabilidad de cazar la mosca es igual al porcentaje de espacio que es capaz de cubrir con su matamoscas:
\[p = \frac{l}{1} = 0.8\]
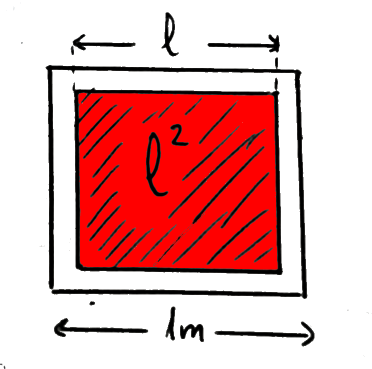
Imaginemos que Minsky vive ahora un espacio bi-dimensional, un plano de dimensiones 1 m \(\times\) 1 m, y que su cazamoscas es de 0.8 m \(\times\) 0.8 m. La probabilidad de cazar la mosca es ahora:
\[p = \frac{l^2}{1} = 0.8^2\]
Es curioso. El area de salvación de la mosca cada vez es más y más voluminosa en detrimento del espacio ocupado por el cazamoscas. De hecho, si seguimos subiendo de dimensiones, la probabilidad de cazar la mosca en d-dimensiones es:
\[p = l^d\]La gráfica muestra como esta probabilidad se va desvanenciendo a medida que subimos en número de dimensiones.
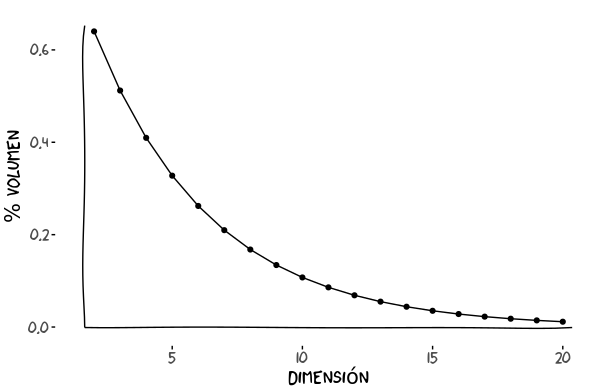
¡Parece que es altas dimensiones no hay manera de cazar una mosca!
Esta imágen ilustra la misma idea. A medida que subimos en dimensiones, el segmento resaltado (el cazamoscas), representa una parte más pequeña del total y la mosca tiene más espacio para campar a sus anchas:
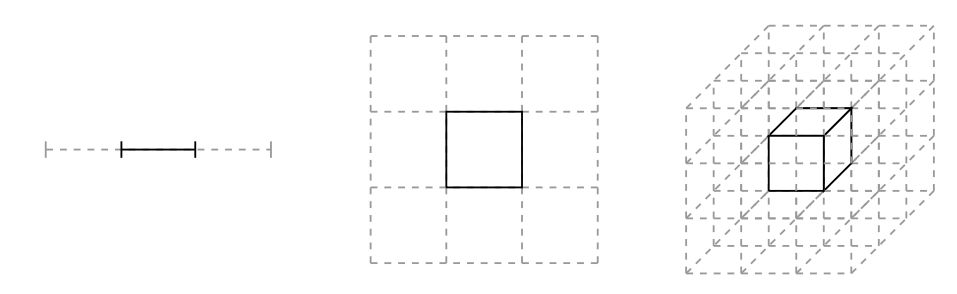
Goteras multidimensionales
Vamos a por un segundo ejemplo donde jugaremos con esferas en lugar de cubos. Imaginemos que tenemos goteras por todo el techo en nuestro comedor de dimensiones 1 m \(\times\) 1 m y que queremos recoger todo el agua posible. Para ello ponemos un barreño 1 m de diámetro. El porcentaje de agua que caerá fuera del barreño es el cociente entre la superficie del barreño y la superficie del comedor. Esto es:
\[p = \frac{\pi R^2}{1} = \frac{\pi 0.5^2}{1} = \frac{\pi}{4} \approx 0.78\]
Es decir, sólo un 22% del agua caerá fuera (puntos rojos)
¿Qué pasa en \(d\)-dimensiones?
\[p = \frac{ \frac{\pi^{d/2}}{\Gamma(\frac{d}{2} +1)}R^d}{1} = \frac{\pi^{d/2}}{\Gamma(\frac{d}{2} +1)}R^d\]donde el numerador es el volumen de una esfera de radio R.
Mirando la gráfica vemos que a partir de la dimensión 4 ya cae más agua fuera que dentro!
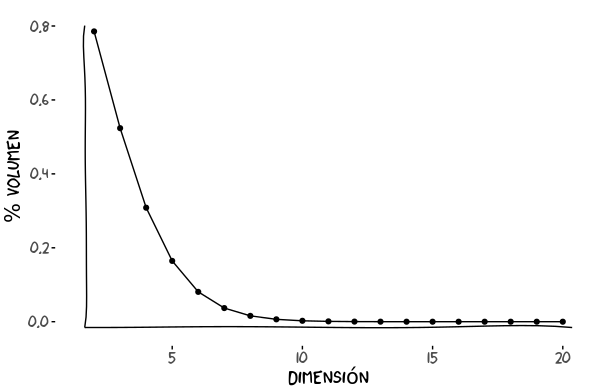
Volviendo al ejemplo del melón en una caja: a más dimensiones tenga la caja, más proporción de aire y menos de melón.
Dardos, fútbol y puntería multidimensional en general
Esta dificultad de hacer puntería en altas dimensiones se reproduce en todas partes. En una diana de darnos multidimensional, la probabilidad de hacer diana (si no tocamos el diámetro de esta) tiende a cero. Lo mismo pasa, en fútbol, a la probabilidad de meter un gol (a no ser que aumentemos las medidas de la portería a medida que subimos de dimensiones). Y en basket, la probabilidad de meter una canasta también de desvanece.
Hacer deporte en altas dimensiones es muy, muy aburrido.
Aprendizaje automático: espacios desérticos y vecindarios vacios
En aprendizaje automático el problema es el siguiente. Imaginemos que me dan una lista de animales descritos por su peso y su altura y una etiqueta que indica si el animal es un gato o un perro. Por simplicidad asumiremos que los atributos tienen tres valores posibles: bajo, medio, alto. El número de combinaciones posibles es:
\[3~\text{pesos} \times 3~\text{alturas} = 3^2\]Con unas decenas de ejemplos empezaré a ser capaz de ver qué combinaciones de atributos tienen a ser de perros y qué combinaciones tienden a ser de gatos.
Ahora, para poder mejorar mi clasificador, me dan cuatro atributos más: tamaño de las orejas, longitud de la cola, cantidad de pelo, y número de horas durmiendo… A priori parece útil, pero si no me dan más ejemplos no me están haciendo ningún favor. Mi espacio de ha crecido brutalmente! Ahora el número de combinaciones es:
\[3~\text{pesos} \times 3~\text{alturas} \times ~ ... = 3^6\]Si antes tenía 9 combinaciones posibles ahora tenemos 729. El problema es que si sólo nos dan 10 ejemplos, la mayoría de combinaciones están quedando inexploradas.
Vemos entonces que en altas dimensiones, todo está lejos de todo. Esto nos lleva un problema añadido, y es que desaparece la noción de vecindad (en el sentido de distancia en sus atributos, es decir, de parecerse) tan útil en aprendizaje. Si todo está lejos de todo, entonces un punto no tiene vecinos (puntos parecidos) y no podré decir si es un gato o un perro. “Pero el vecindario está definido arbitrariamente, aumentemos el radio del vecindario!”, dirán algunos. El problema es que si nuestro radio de vecindario es muy grande acabamos considerando que todos son vecinos de todos, lo cual es tan inútil como considerar que todos son vecinos de todos.
En resumen, el aumento de dimensiones me desertifica el espacio, me lo convierte en un Mad Max multidimensional.
Tenemos dos soluciones a este problema: usar menos atributos o conseguir más ejemplos.
Distribuciones de probabilidad: sets típicos
La maldición de la multidimensionalidad tiene también su efecto en distribuciones de probabilidad (Gaussianas, Poisson, etc): la moda deja de ser interesante.
La moda de una distribución es el punto con mayor densidad de probabilidad. Sin embargo, más que la densidad la medida que realmente nos interesa es la masa, calculada como el producto de la densidad por el volumen (ver imagen):
\[\text{masa} = \text{densidad} \times \text{volumen}\]
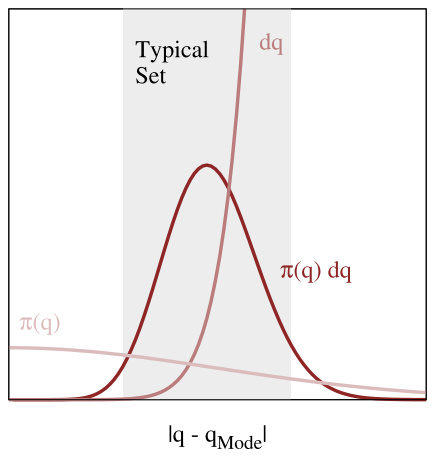
En la imagen se muestra un ejemplo (inventado) de densidad (\(\pi(q)\)), volumen (de cada cachito del espacio, dq) y su producto. Vamos a analizar que pasa con dos de las distribuciones de probabilidad más conocidas: la Uniforme y la Gaussiana.
- Distribución uniforme
La distribución uniforme la hemos tocado implícitamente antes, cuando hablábamos de las goteras: dado un suelo de dimensiones \(d_1 \times d_2\), las gotas tienen la misma probabilidad de caer en todas las partes del suelo. Hemos visto que, a medida que subíamos de dimensiones, la mayoría de gotas caían en los bordes del suelo. En otras palabras, es más probable que una gota caiga en el algún punto del borde que justo en el centro.
Podemos pensar en una granada (la fruta). Imaginemos que le vamos quitando las pepitas de fuera hacia dentro, rotando la granada en nuestras manos. En las primeras rotaciones obtendremos más pepitas que en las últimas!

O en una cebolla, que es también uniformemente densa y cuyas capas externas tienen más masa que las capas internas:

La distribución uniforme asigna la misma densidad probabilidad a cualquier punto del espacio. A medida que nos alejamos del centro, el volumen aumenta y la densidad se mantiene, por lo que la masa es mayor a más nos alejemos del centro. De ahí el fenómeno de las goteras que caían más fuera que dentro del barreño.
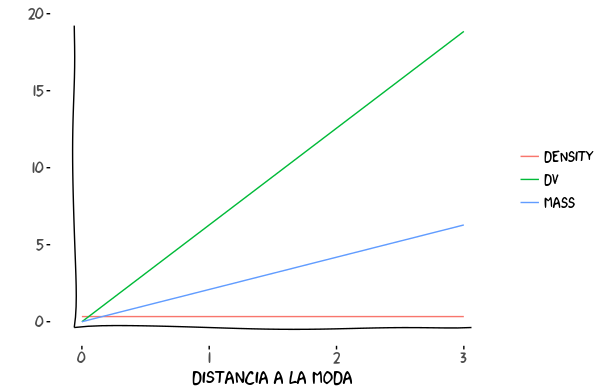
Con muchas dimensiones, el volumen crecerá más rápido a medida que nos alejamos de la moda, por lo que el producto de volumen por densidad, la masa, crecerá aún más rápido.
- Distribución Gaussiana
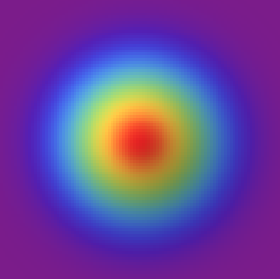
¿Qué pasaría si las goteras siguieran una forma de gaussiana en el techo? El volumen aumenta a medida que nos alejamos del centro, pero por otro lado la densidad va bajando. La región con mayor agua vendrá marcada por el producto de los dos.
En dos dimensiones, la carga del volumen empieza a desplazarse hacia valores más lejanos del centro. ¿Dónde está la mayor parte de la masa?
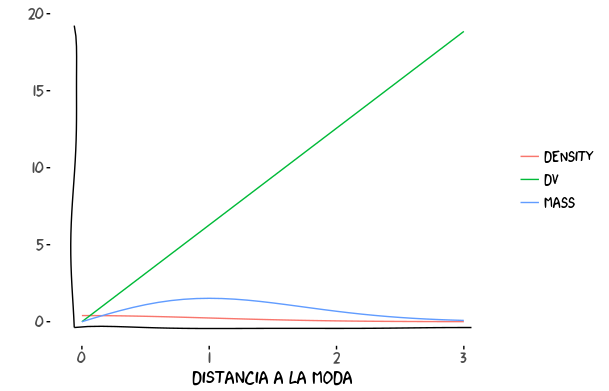
Igual que antes, en muchas dimensiones el volumen crecerá más rápido a medida que nos alejamos de la moda. El efecto en la Gaussiana es que la montañita que indica la zona de más mas (conocido como set típico) se irá alejando más y más a la derecha, divorciándose de la moda.
Y es por eso que cuando se tienen muchas variables calcular la esperanza (valor que tiene en cuenta la masa) es mejor idea que buscar la moda.
Conclusión
La maldición de la dimensionalidad es un fenómeno que afecta muchos problemas matemáticos. Geométricamente, el fenómeno puede resumirse como un melón en una caja multidimensionales donde hay más volumen de aire que de melón.
En estadistica y aprendizaje automático, aumentar el número de variables de un problema puede parecer una buena idea pero, si no se acompaña de más observaciones, puede empeorar las cosas y convertir nuestro espacio en un desierto donde el aprendizaje y las inferencias estadísticas se complican.