Generating distributions with the Stick Breaking version of the Dirichlet Process
Posted on 28 Jun 2018
The Dirichlet Process is a prior over distributions. The basic definition relays on measure theory and has some obscure definitions for most of people. Intuitevily, imagine we want to draw a distribution \(G\) over the line of real numbers using some prior distribution \(P\). We say that \(P\) is a Dirichlet Process if, for any possible partition of the line of real numbers, \((A_1, ..., A_m)\), the probabilities over the partitions are distributed according to a Dirichlet distribution:
\[G(A_1),...,G(A_m) \sim \text{Dirichlet}(\alpha(A_1),...,\alpha(A_k))\]There are different ways to generate a distribution G. One of the most popular is the Stick Breaking construction. The trick is to realize that
\[G = \sum_k \pi_k \delta_{\theta_k}\]where \(\pi_k\) weights sum up to 1, and the deltas are distributed around the line of the real numbers according to some distribution. The stick breaking construction goes as follows:
-
Take a stick of length 1 and make infinite random breaks. Each break removes a percentage \(v_k\) of the remaining stick
\[v_k \sim \text{Beta}(1, \alpha)\]The length of the removed break is
\[\pi_k = v_k \prod_{i=1}^{k-1}(1-v_i)\]where \(\prod_{l=1}^{k-1}(1-v_l)\) is the remaining length of the stick at step \(k\). At the end of the process we have a collection of segments whose length sum is 1.
-
Draw infinite samples from a base distribution \(G_0\):
\[\phi_k \sim G_0\]where \(G_0\) can be any distribution such as a Gaussian, a Poisson or a Multinomial.
-
We build our distribution as
\[G = \sum_{k=1}^\infty \pi_k \delta_{\phi_k}\]
Here is the R code to sample from a Dirichlet Process using the Stick Breaking construction:
library(dplyr)
library(ggplot2)
#'@title Stick Breaking construction of a Dirichlet Process
#'@param n number of samples
#'@param alpha concentration parameter
#'@param G0 base measure
DP_stick_breaking <- function(n, alpha, G0) {
# Stick breaking
v <- rbeta(n, 1, alpha)
pi <- numeric(n)
pi[1] <- v[1]
pi[2:n] <- sapply(2:n, function(i) v[i] * prod(1 - v[1:(i-1)]))
# Atoms from the base measure
y <- G0(n)
return(list(atoms = y,
pis = pi))
# Sample from the Dirichlet Process G
#theta <- sample(y, prob = pi, replace = TRUE)
#return(theta)
}
# Choose a base distribution
G0 <- function(n) rpois(n, 7) # Poisson
G0 <- function(n) rnorm(n, 0, 1) # Gaussian
# Concentration parameter around the base distribution
alphas <- c(1, 10, 100, 1000)
n <- 1000
df.G <- as.data.frame(matrix(NA, 0, 4))
names(df.G) <- c("xp", "i", "atom", "pi")
df.samples <- as.data.frame(matrix(NA, 0, 4))
names(df.samples) <- c("xp", "i", "alpha", "samples")
for(alpha in alphas){
for(xp in 1:3){
cat("\n", alpha)
# Generate a distribution from the DP(alpha, G0)
G <- DP_stick_breaking(n, alpha, G0)
df.G <- bind_rows(df.G,
list(xp = rep(xp, n),
alpha= rep(alpha, n),
i=1:n,
atom = G$atoms,
pi=G$pis))
# Generate samples from the DP
samples <- sample(G$atoms, prob = G$pis, replace = TRUE)
df.samples <- bind_rows(df.samples,
list(xp = rep(xp, n),
alpha= rep(alpha, n),
i=1:n,
sample=samples))
}
}
# Plot the distributon drawn by the DP
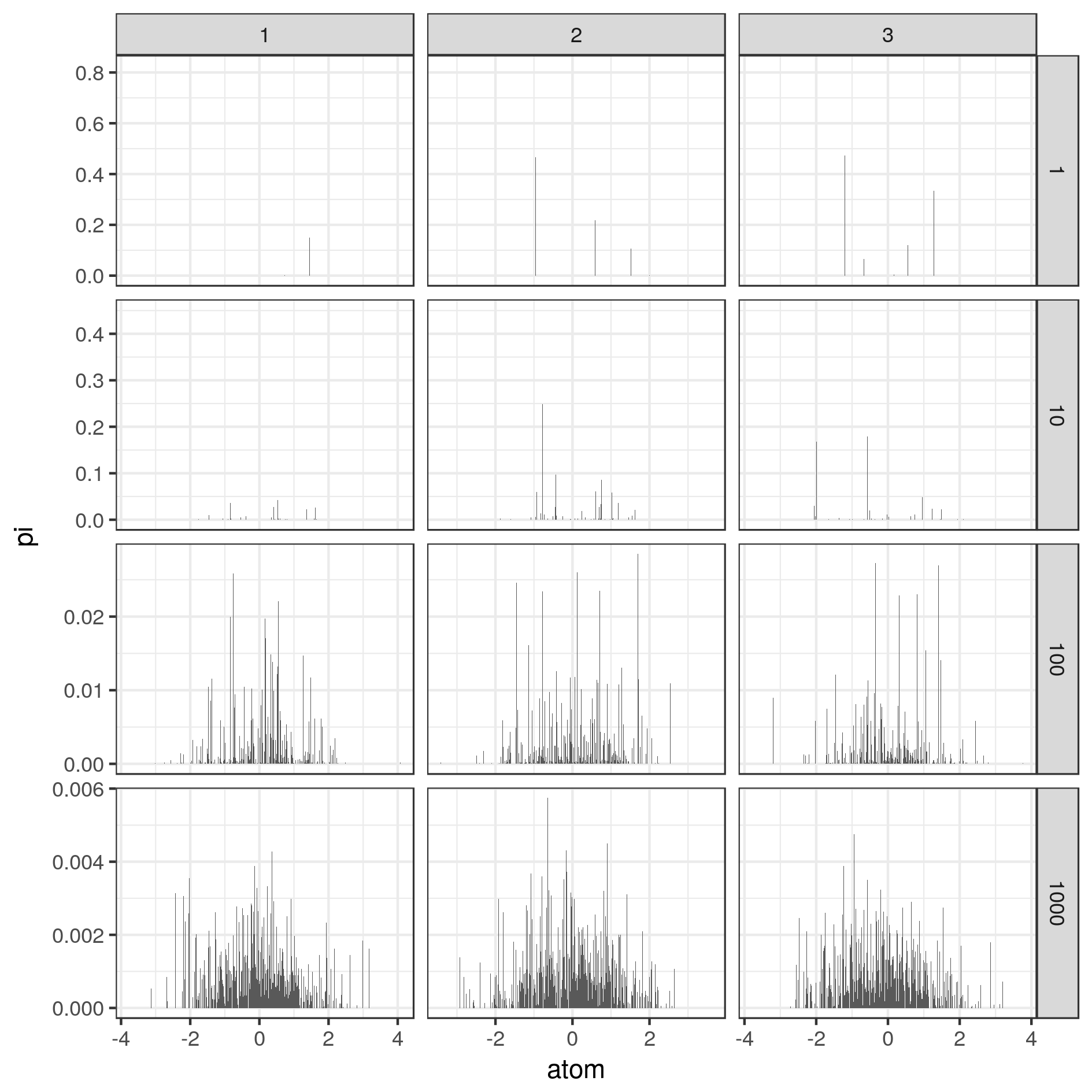
df.G$alpha <- factor(df.G$alpha)
p <- ggplot(df.G, aes(x=atom, y=pi)) +
geom_col(width=0.01)+
facet_grid(alpha ~ xp, scales = "free") +
theme_bw()
print(p)
ggsave(p, filename = paste0("fig15_DP.png"),
height=16, width=16, units='cm')
# Plot samples from the distribution
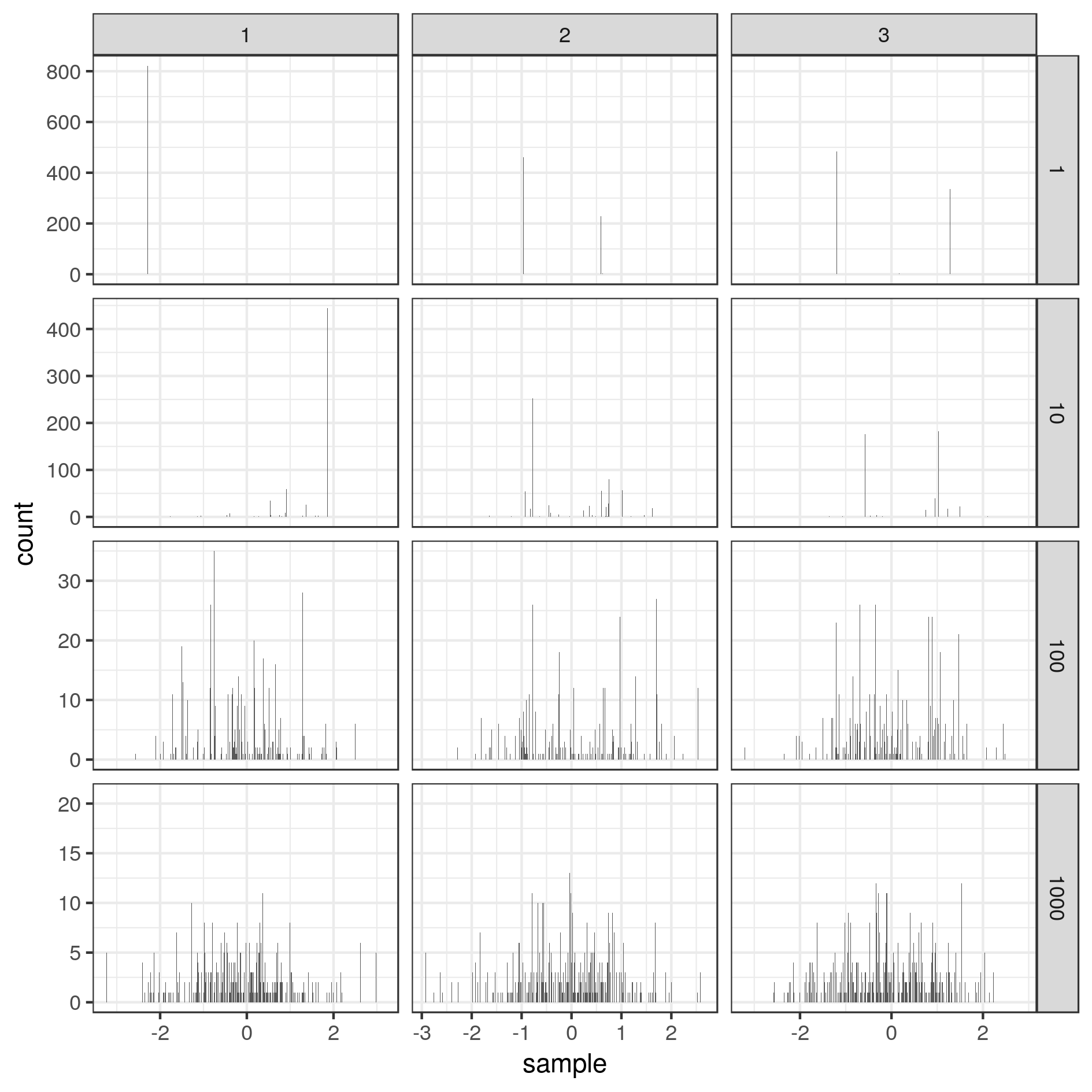
df.samples$alpha <- factor(df.samples$alpha)
p <- ggplot(df.samples, aes(x=sample)) +
#geom_density() +
#geom_histogram(bins=100, aes(y=..count../sum(..count..))) +
geom_histogram(bins=1000) +
facet_grid(alpha ~ xp, scales = "free") +
theme_bw()
print(p)
ggsave(p, filename = paste0("fig16_DPsamples.png"),
height=16, width=16, units='cm')
And here are the results of Dirichlet Process \(G\) generated with the Stick Breaking and different concentration \(\alpha\), and samples obtained from these \(G\):